kak tolong dijawab pliss,, besok di kumpul
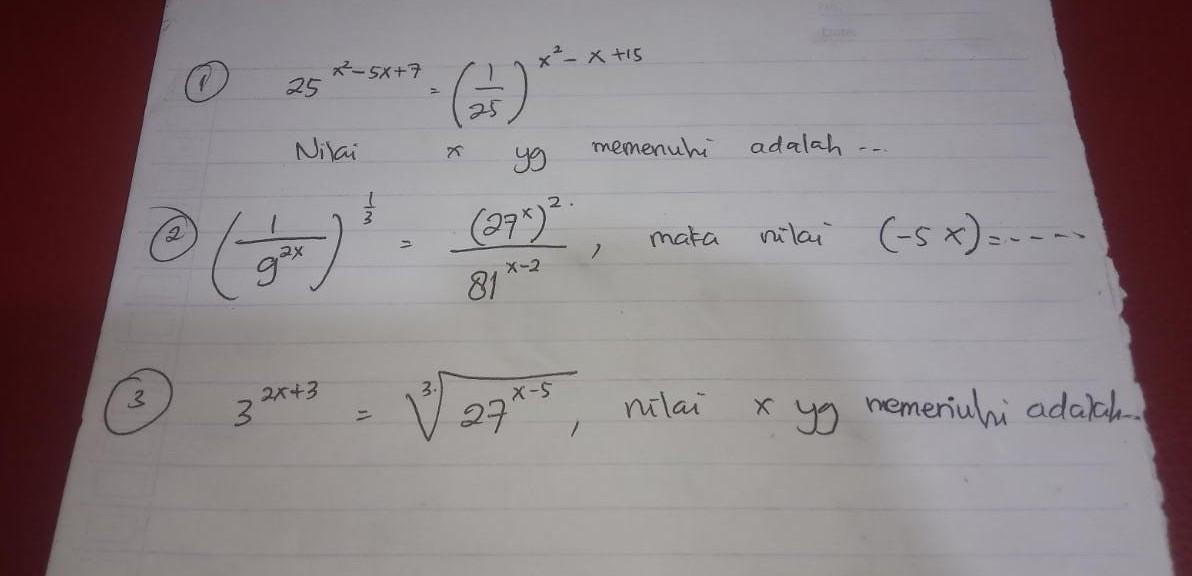
-
Bidang studi:
Matematika -
Penulis:
wiz -
Dibuat:
1 tahun lalu
Jawaban 1
Persamaan Eksponen
- [tex]25^{x^{2} \:-\:5x \:+\: 7} = \left(\frac{1}{25}\right)^{x^{2} \:-\: x \:+\: 15}[/tex]. Nilai x yang memenuhi adalah….
- [tex]\left(\frac{1}{9^{2x}}\right)^{\frac{1}{3}} = \frac{(27^{x})^{2}}{81^{x \:-\: 2}}[/tex], maka nilai (–5x) = ….
- [tex]3^{2x \:+\: 3} = \sqrt[3]{27^{x \:-\: 5}}[/tex]. Nilai x yang memenuhi adalah….
Jawaban untuk soal di atas adalah:
- Tidak ada nilai x bilangan real yang memenuhi persamaan tersebut.
- Nilai dari (–5x) adalah 12.
- Nilai x yang memenuhi adalah x = –6.
Nomor 1
Diketahui
[tex]25^{x^{2} \:-\:5x \:+\: 7} = \left(\frac{1}{25}\right)^{x^{2} \:-\: x \:+\: 15}[/tex]
Ditanyakan
Tentukan nilai x yang memenuhi!
Jawab
[tex]25^{x^{2} \:-\:5x \:+\: 7} = \left(\frac{1}{25}\right)^{x^{2} \:-\: x \:+\: 15}[/tex]
[tex]25^{x^{2} \:-\:5x \:+\: 7} = (25^{-1})^{x^{2} \:-\: x \:+\: 15}[/tex]
[tex]25^{x^{2} \:-\:5x \:+\: 7} = 25^{-x^{2} \:+\: x \:-\: 15}[/tex]
x² – 5x + 7 = –x² + x – 15
2x² – 6x + 22 = 0
x² – 3x + 11 = 0
- a = 1
- b = –3
- c = 11
Nilai diskriminan
D = b² – 4ac
= (–3)² – 4(1)(11)
= 9 – 44
= –35
Diperoleh nilai diskriminannya negatif (D < 0), sehingga tidak ada nilai x real yang memenuhi.
Nomor 2
Diketahui
[tex]\left(\frac{1}{9^{2x}}\right)^{\frac{1}{3}} = \frac{(27^{x})^{2}}{81^{x \:-\: 2}}[/tex]
Ditanyakan
Tentukan nilai dari (–5x)!
Jawab
[tex]\left(\frac{1}{9^{2x}}\right)^{\frac{1}{3}} = \frac{(27^{x})^{2}}{81^{x \:-\: 2}}[/tex]
[tex]\left(\frac{1}{(3^{2})^{2x}}\right)^{\frac{1}{3}} = \frac{27^{2x}}{(3^{4})^{x \:-\: 2}}[/tex]
[tex]\left(\frac{1}{3^{4x}}\right)^{\frac{1}{3}} = \frac{(3^{3})^{2x}}{3^{4x \:-\: 8}}[/tex]
[tex](3^{-4x})^{\frac{1}{3}} = \frac{(3^{6x}}{3^{4x \:-\: 8}}[/tex]
[tex]3^{-\frac{4x}{3}} = 3^{6x \:-\: (4x \:-\: 8)}[/tex]
[tex]3^{-\frac{4x}{3}} = 3^{6x \:-\: 4x \:+\: 8}[/tex]
[tex]3^{-\frac{4x}{3}} = 3^{2x \:+\: 8}[/tex]
[tex]-\frac{4x}{3} = 2x \:+\: 8[/tex]
–4x = 3(2x + 8)
–4x = 6x + 24
–10x = 24
==> kedua ruas dibagi 2 <==
–5x = 12
Nomor 3
Diketahui
[tex]3^{2x \:+\: 3} = \sqrt[3]{27^{x \:-\: 5}}[/tex]
Ditanyakan
Tentukan nilai x yang memenuhi!
Jawab
[tex]3^{2x \:+\: 3} = \sqrt[3]{27^{x \:-\: 5}}[/tex]
[tex]3^{2x \:+\: 3} = \sqrt[3]{(3^{3})^{x \:-\: 5}}[/tex]
[tex]3^{2x \:+\: 3} = \sqrt[3]{3^{3x \:-\: 15}}[/tex]
[tex]3^{2x \:+\: 3} = 3^{\frac{3x \:-\: 15}{3}}[/tex]
[tex]2x \:+\: 3 = \frac{3x \:-\: 15}{3}[/tex]
3(2x + 3) = 3x – 15
6x + 3 = 3x – 15
3x = –18
x = –6
Pelajari lebih lanjutMateri tentang himpunan penyelesaian dari persamaan eksponen https://brainly.co.id/tugas/13536276
#BelajarBersamaBrainly #SPJ1
-
Penulis:
timoteoblake
-
Nilai jawaban:
9

