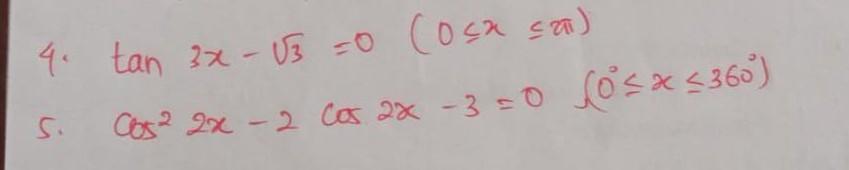KPK dari 28 dan 36 adalah?​

12,7

3,5

____

835

381

____

46,45

karena dibelakang koma 7 dan 5 maka jadi 46,45

Jawaban:

Sebagai suatu perangkat lunak (software) dalam komputer, sistem operasi memiliki beberapa fungsi penting dan tanpa adanya sistem operasi maka komputer tidak dapat menjalankan program dan fungsinya. 

Untuk mengisi titik-titik pada pertanyaan, menurut saya ada beberapa jawaban yang benar dan memungkinkan.

• Pertama, sistem operasi adalah perangkat lunak atau software.
• Kedua, sistem operasi adalah perangkat lunak sistem atau system software.Alternatif kedua ini terkait langsung dengan subkalimat “tanpa adanya sistem operasi maka komputer tidak dapat menjalankan program dan fungsinya”, karena fungsi dari sebuah system software adalah sebagai interface yang menghubungkan user application (aplikasi yang terpasang di dalamnya, seperti aplikasi pengolah kata, grafis, dsb.) dengan komponen perangkat keras komputer, sehingga user application dapat berfungsi sebagaimana mestinya. Artinya: user application dapat menerima input, memprosesnya, dan menghasilkan output dengan benar, sesuai fungsi dan mekanisme yang diimplementasikan.

Tentukan nilai x untuk persamaan trigonometri

• [tex]tan \: 3x \:-\: \sqrt{3} \:=\: 0[/tex], (0 ≤ x ≤ 2π)
• [tex]cos^2 \: 2x \:-\: 2 cos \: 2x \:-\: 3 \:=\: 0[/tex], (0° ≤ x ≤ 360°)

Himpunan penyelesaian nilai x untuk persamaan trigonometri adalah

• HP = {20°, 80°, 140°, 200°. 260°, 320°}
• HP = {90°, 270°}

Penjelasan dengan langkah-langkah:

Diketahui:

• Soal pada lampiran.

Ditanyakan:

• HP?

Jawaban:

4. Persamaan tangen berlaku

• tan x = tan a
• x = a + 180° k, k = 1, 2, 3,...

[tex]tan \: 3x \:-\: \sqrt{3} \:=\: 0[/tex]

[tex]tan \: 3x \:=\: \sqrt{3}[/tex]

[tex]tan \: 3x \:=\: tan \: 60^o[/tex]

[tex]3x \:=\: 60^o \:+\: 180^o k[/tex]

[tex]x \:=\: \frac{60^o}{3} \:+\: \frac{180^o}{3} k[/tex]

[tex]x \:=\: 20^o \:+\: 60^o k[/tex]

• k = 0 ⇒ x = 20° + 0 = 20°
• k = 1 ⇒ x = 20° + 60 = 80°
• k = 2 ⇒ x = 20° + 120 = 140°
• k = 3 ⇒ x = 20° + 180 = 200°
• k = 4 ⇒ x = 20° + 240 = 260°
• k = 5 ⇒ x = 20° + 300 = 320°
• k = 6 ⇒ x = 20° + 360 = 380°, tidak masuk dalam himpunan karena lebih dari 2π

HP = {20°, 80°, 140°, 200°. 260°, 320°}

5. Persamaan cosinus berlaku

• cos x = cos a
• x = a + 360° k, k = 1, 2, 3,...
• x = - a + 360° k, k = 1, 2, 3,...

[tex]cos^2 \: 2x \:-\: 2 cos \: 2x \:-\: 3 \:=\: 0[/tex]

Misalkan cos 2x = p

[tex]p^2 \:-\: 2p \:-\: 3 \:=\: 0[/tex]

[tex](p \:-\: 3) \: (p \:+\: 1) \:=\: 0[/tex]

p - 3 = 0     atau p + 1 = 0

p = 3           atau p = - 1

cos 2x = 3  atau cos 2x = - 1

Nilai cos berkisar antara - 1 sampai 1, maka tidak mungkin ada nilai x yang memenuhi cos 2x = 3.

cos 2x = - 1

[tex]cos \: 2x \:=\: cos \: 180^o[/tex]

[tex]2x \:=\: 180^o \:+\: 360^o k[/tex]

[tex]x \:=\: \frac{180^o}{2} \:+\: \frac{360^o}{2} k[/tex]

[tex]x \:=\: 90^o \:+\: 180^o k[/tex]

• k = 0 ⇒ x = 90° + 0 = 90°
• k = 1 ⇒ x = 90° + 180 = 270°
• k = 2 ⇒ x = 90° + 360 = 450°, tidak termasuk HP.

HP = {90°, 270°}

Pelajari lebih lanjut

• Pelajari lebih lanjut tentang materi Persamaan Trigonometri https://brainly.co.id/tugas/42268493

#BelajarBersamaBrainly

#SPJ1

3 : 4/7

= 3 × 7/4

= 21/4

= 5 1/4

Penjelasan dengan langkah-langkah:

[tex] \\ \\ \\ [/tex]

[tex]3 \div \frac{4}{7} \\ [/tex]

[tex] = 3 \times \frac{7}{4} \\ [/tex]

[tex] = \frac{21}{4} \\ [/tex]

[tex] {\tt \green {= 5 \frac{1}{4} }} \\ [/tex]

[tex] \\ \\ \\ [/tex]