1 ½ : 3 ⅓ : 3/5= PAKAI CARA YA KA!buat YANG GATAU GAUSAH dijawab
-
Bidang studi:
Matematika -
Penulis:
colbynewman -
Dibuat:
1 tahun lalu
Jawaban 2
Jawaban:
semoga mudah dimengerti
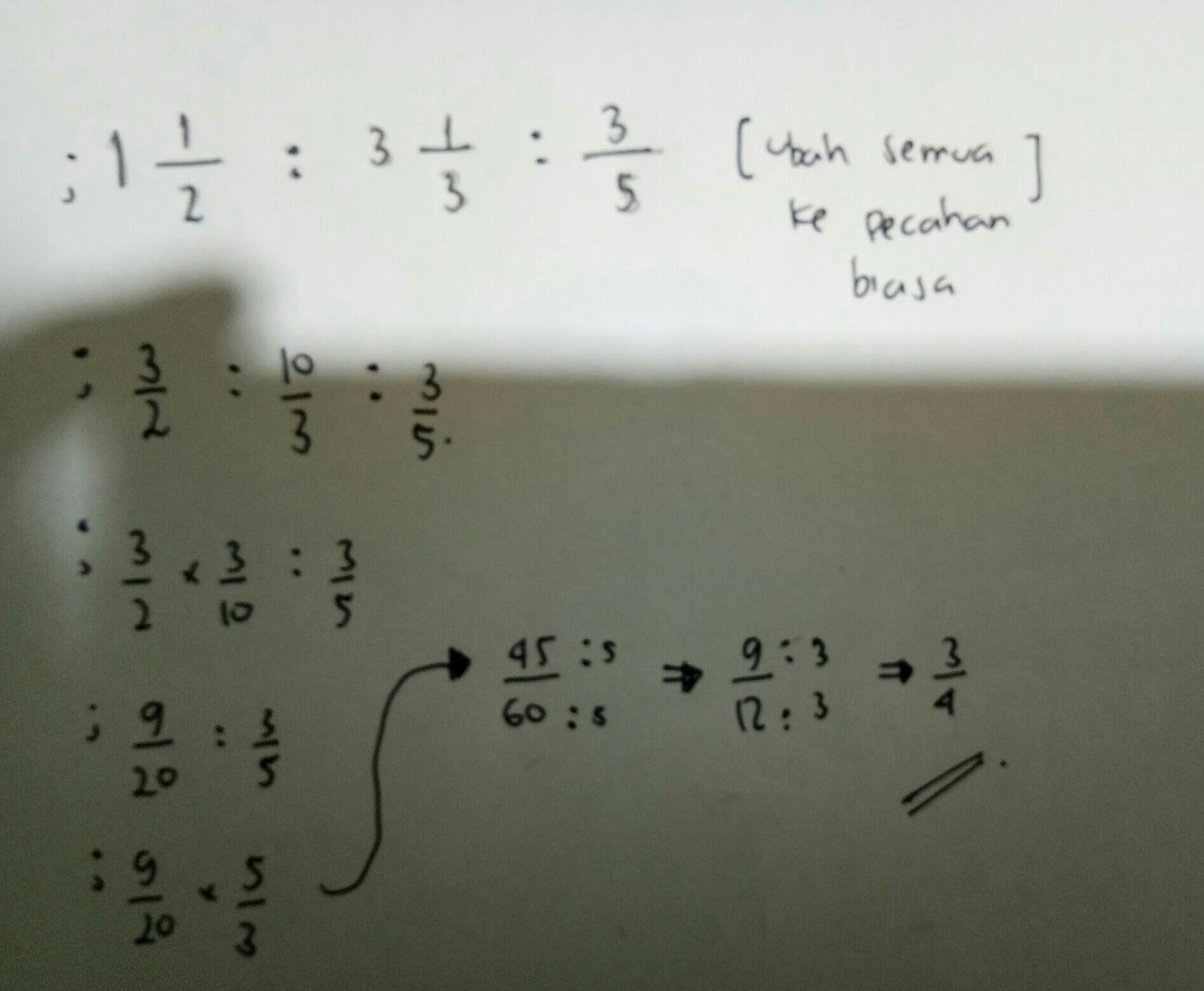
-
Penulis:
lunag5s3
-
Nilai jawaban:
7
Penjelasan dengan langkah-langkah:
ini loh gak pakai cara selamat mengerjakan

-
Penulis:
begoña3kje
-
Nilai jawaban:
6
Apakah kamu tahu jawabannya? Tambahkan di sini!
Pilih bahasa dan wilayah
How much to ban the user?
1 hour
1 day
100 years

