Jika suatu barisan aritmatika dengan [tex]\text U_3 = 11[/tex], dan [tex]\text U_5 = 17[/tex]. Maka tentukan;
a. Barisan bilangannya : 8, [tex]9\frac{1}{2}[/tex], 11, [tex]12\frac{1}{2}[/tex] , . . . .
b. Jumlah 6 suku pertama adalah [tex]\text S_{6} = 70\frac{1}{2}[/tex]
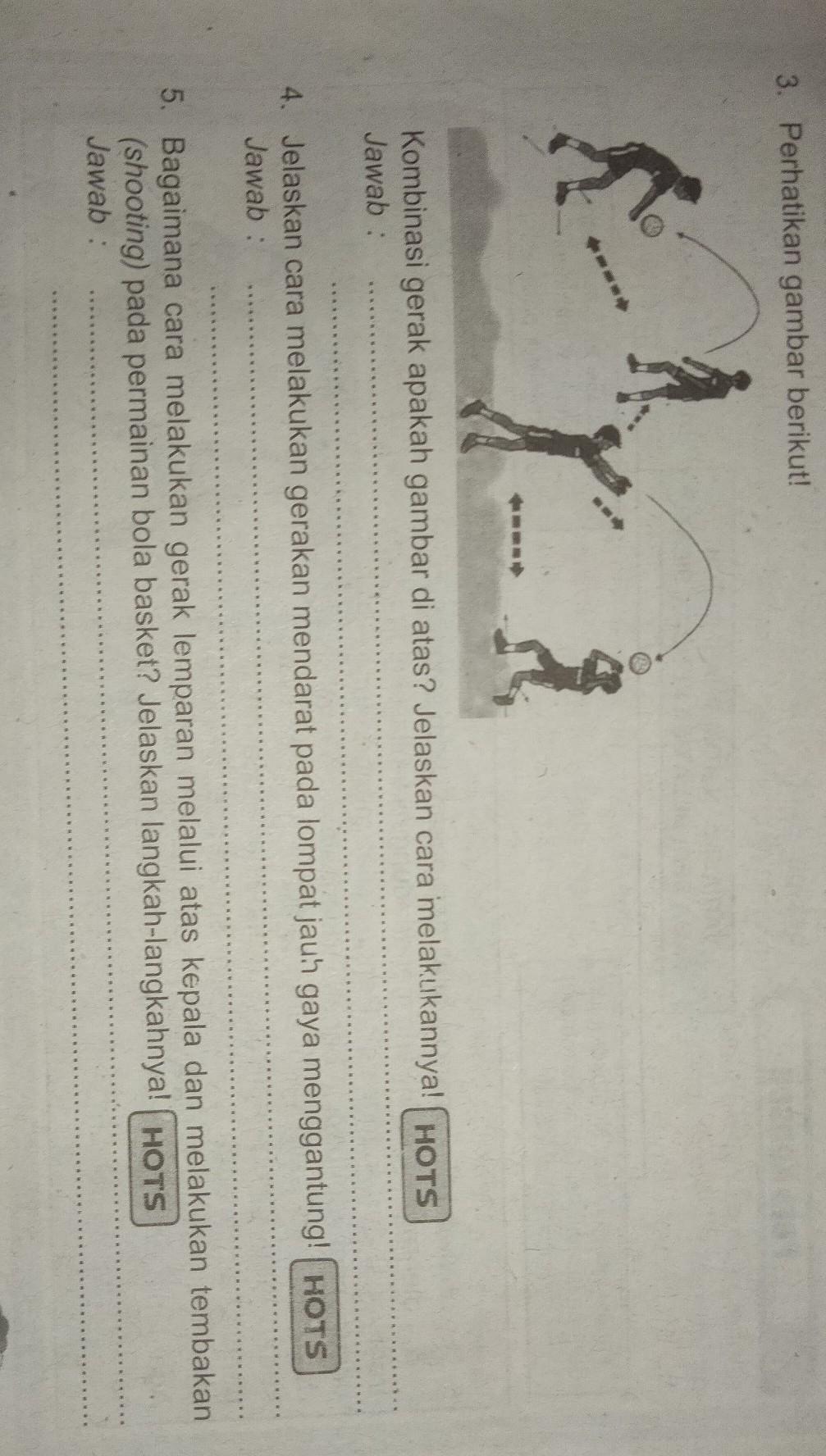
Pendahuluan
Barisan aritmatika merupakan suatu barisan bilangan dengan nilai setiap sukunya didapat dari suku sebelumnya. Caranya yaitu dengan mengurangkan atau menjumlahkan suatu bilangan tetap. Selisih antara nilai suku-suku yang berdekatan selalu tetap yang selanjutnya disebut beda (b).
Pembahasan
Rumus suku ke-n barisan aritmatika : [tex]\boxed{\text U_\text n~=~\text a + (\text n - 1)\text b}[/tex]
Rumus jumlah n suku pada deret aritmatika
[tex]\boxed {\text S_{\text n} = \frac{\text n}{2} (~2\text a + (\text n - 1)\text b~)}[/tex] atau [tex]\boxed {\text S_{\text n} = \frac{\text n}{2} (~\text a + \text U_{\text n})}[/tex]
Keterangan :
a = suku awal/suku pertama
b = beda = [tex]\text U_2 - \text U_1[/tex]
n = banyak suku
[tex]\text U_\text n[/tex] = suku ke-n
Penyelesaian
Diketahui :
Barisan aritmatika
[tex]\text U_{3} = 11[/tex]
[tex]\text U_{7} = 17[/tex]
Ditanyakan :
a. Barisan bilangan :
b. Nilai [tex]\text S_{6}[/tex] = . . . .
Jawab :
Menentukan nilai a (suku awal) dan b (beda)
[tex]\text U_{3} = 11[/tex] maka a + 2b = 11
[tex]\text U_{7} = 17[/tex] maka a + 6b = 17
Eliminasi a
a + 2b = 11
a + 6b = 17 -
-4b = -6
b = [tex]\displaystyle \frac{6}{4}[/tex]
b = [tex]\displaystyle \frac{3}{2}[/tex]
Nilai b = [tex]\displaystyle \frac{3}{2}[/tex] disubstitusikan ke a + 2b = 11
a + 2b = 11
a + 2( [tex]\displaystyle \frac{3}{2}[/tex]) = 11
a + 3 = 11
a = 11 - 3
a = 8
Menentukan barisan bilangan
Untuk a = 8 dan b = [tex]\displaystyle \frac{3}{2}[/tex] maka [tex]\text U_\text n = \text a + (\text n - 1)\text b[/tex]
[tex]\text U_\text n = \text a + (\text n - 1)\text b[/tex]
⇔ [tex]\text U_\text n = 8 + (\text n - 1)\frac{3}{2}[/tex]
⇔ [tex]\text U_\text n = 8 + \frac{3}{2} \text n - \frac{3}{2}[/tex]
⇔ [tex]\text U_\text n = \frac{3}{2} \text n + \frac{13}{2}[/tex]
[tex]\text U_1[/tex] = 8
[tex]\text U_2 = \frac{3}{2} (2) + \frac{13}{2} = 3 + \frac{13}{2} = 9\frac{1}{2}[/tex]
[tex]\text U_3 = \frac{3}{2} (3) + \frac{13}{2} = \frac{9}{2} + \frac{13}{2} = 11[/tex]
[tex]\text U_4 = \frac{3}{2} (4) + \frac{13}{2} = 6 + \frac{13}{2} = 12\frac{1}{2}[/tex]
∴ Barisan bilangannya adalah 8, [tex]9\frac{1}{2}[/tex], 11, [tex]12\frac{1}{2}[/tex] , . . . .
Menentukan [tex]\text S_{6}[/tex]
Untuk a = 8, b = [tex]\displaystyle \frac{3}{2}[/tex] , n = 6, maka :
[tex]\text S_{\text n} = \frac{\text n}{2} (~2\text a + (\text n - 1)\text b)[/tex]
⇔ [tex]\text S_{6} = \frac{6}{2} (2(8) + (6 - 1)(\frac{3}{2} ))[/tex]
⇔ [tex]\text S_{6} = 3 (16 + 5(\frac{3}{2} ))[/tex]
⇔ [tex]\text S_{6} = 3 (16 + \frac{15}{2} )[/tex]
⇔ [tex]\text S_{6} = 3 (\frac{47}{2} )[/tex]
⇔ [tex]\text S_{6} = \frac{141}{2}[/tex]
⇔ [tex]\text S_{6} = 70\frac{1}{2}[/tex]
∴ Jadi nilai [tex]\text S_{6} = 70\frac{1}{2}[/tex]
Pelajari lebih lanjut :
- Pengertian barisan aritmatika : https://brainly.co.id/tugas/1509694
- Menentukan suku ke-n : https://brainly.co.id/tugas/12054249
- Contoh soal barisan aritmatika : https://brainly.co.id/tugas/1168886
- Deret aritmatika : https://brainly.co.id/tugas/13759951
- Pelajari juga : https://brainly.co.id/tugas/25343272
- Barisan aritmatika : https://brainly.co.id/tugas/50489229
_______________________________________________________
Detail Jawaban
Kelas : IX - SMP
Mapel : Matematika
Kategori : Bab 2 - Barisan dan Deret Bilangan
Kode : 9.2.2
Kata kunci : Barisan aritmatika, suku pertama, beda, suku ke-n
#BelajarBersamaBrainly
#CerdasBersamaBrainly