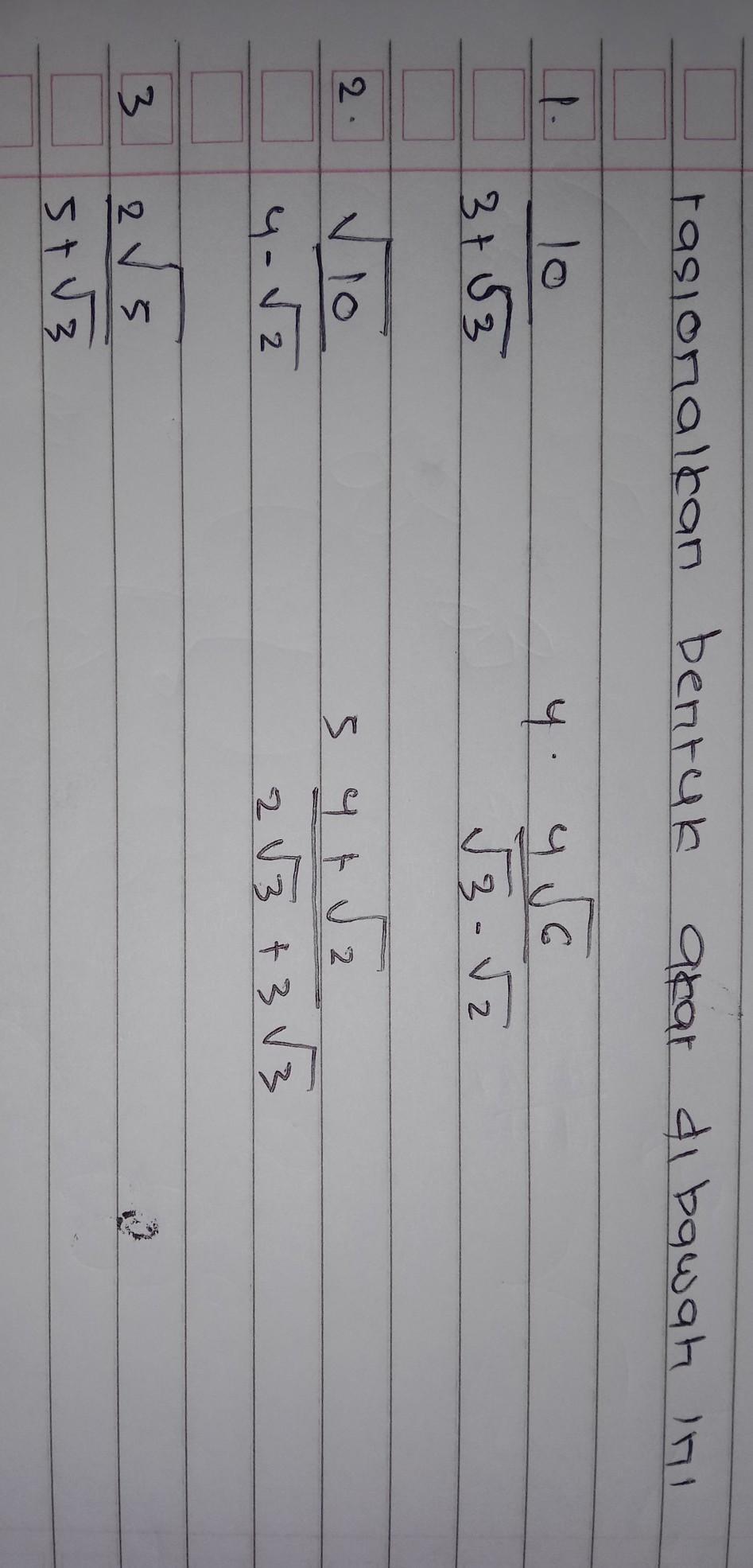Q.membiasakan perilaku sesuai nilai nilai pancasila dalam lingkungan keluarga. perilaku yang sesuai nilai nilai pancasila yang dapat dilakukan dalam lingkungan keluarga antara lain, sebagai berikut. a. Taat dan patuh terhadap orang tua b. ...................................................................c. ...................................................................d. ...................................................................​

Jawaban:

a. Titik-titik koordinat A, B, C, dan D digambarkan pada bidang koordinat Cartesius. Maka, titik-titik tersebut akan membentuk bangun persegi panjang. Perhatikan gambar di attachment.

b. Titik-titik koordinat E, F, G, dan H akan membentuk persegi panjang, jika:

• ditarik garis dari E dua satuan ke atas, dan
• ditarik garis dari G empat satuan ke kiri.

a. bangun yang terbentuk adalah persegi panjang.

b. koordinat titik H agar terbentuk bangun persegi panjang adalah (8, 5).

Jawaban:

pohon pisang

tanaman jeruk

pohon kelapa

pohon apel

Penjelasan:

maaf kalo salah

Jawaban:

tebu,sagu dan enau

Penjelasan:

semoga membantu ya

Terdapat beberapa bentuk akar. Hasil merasionalkan bentuk-bentuk akar tersebut adalah sebagai berikut:

1. [tex]\frac{10}{3+\sqrt{3}}=\bf5-\frac{5}{3}\sqrt{3}[/tex]
2. [tex]\frac{\sqrt{10}}{4-\sqrt{2}}=\bf\frac{2}{7}\sqrt{10}+\frac{1}{7}\sqrt{5}[/tex]
3. [tex]\frac{2\sqrt{5}}{5+\sqrt{3}}=\bf\frac{5}{11}\sqrt{5}-\frac{1}{11}\sqrt{15}[/tex]
4. [tex]\frac{4\sqrt{6}}{\sqrt{3}-\sqrt{2}}=\bf12\sqrt{2}+8\sqrt{3}[/tex]
5. [tex]\frac{4+\sqrt{2}}{2\sqrt{3}+3\sqrt{3}}=\bf\frac{4}{15}\sqrt{3}+\frac{1}{15}\sqrt{6}[/tex]

Diketahui:

1. [tex]\frac{10}{3+\sqrt{3}}[/tex]
2. [tex]\frac{\sqrt{10}}{4-\sqrt{2}}[/tex]
3. [tex]\frac{2\sqrt{5}}{5+\sqrt{3}}[/tex]
4. [tex]\frac{4\sqrt{6}}{\sqrt{3}-\sqrt{2}}[/tex]
5. [tex]\frac{4+\sqrt{2}}{2\sqrt{3}+3\sqrt{3}}[/tex]

Ditanya: hasil perasionalan bentuk akar

Jawab:

Untuk nomor 1:

• Bentuk sekawan penyebut

3-√3

• Hasil perasionalan

[tex]\frac{10}{3+\sqrt{3}}=\frac{10}{3+\sqrt{3}}\cdot\frac{3-\sqrt{3}}{3-\sqrt{3}}\\=\frac{10(3-\sqrt{3})}{3^2-(\sqrt{3})^2}\\=\frac{10(3-\sqrt{3})}{9-3}\\=\frac{10(3-\sqrt{3})}{6}\\=\frac{5(3-\sqrt{3})}{3}\\=\frac{15-5\sqrt{3}}{3}\\=5-\frac{5}{3}\sqrt{3}[/tex]

Untuk nomor 2:

• Bentuk sekawan penyebut

4+√2

• Hasil perasionalan

[tex]\frac{\sqrt{10}}{4-\sqrt{2}}=\frac{\sqrt{10}}{4-\sqrt{2}}\cdot\frac{4+\sqrt{2}}{4+\sqrt{2}}\\=\frac{4\sqrt{10}+\sqrt{20}}{4^2-(\sqrt{2})^2}\\=\frac{4\sqrt{10}+2\sqrt{5}}{16-2}\\=\frac{4\sqrt{10}+2\sqrt{5}}{14}\\=\frac{2\sqrt{10}+\sqrt{5}}{7}\\=\frac{2}{7}\sqrt{10}+\frac{1}{7}\sqrt{5}[/tex]

Untuk nomor 3:

• Bentuk sekawan penyebut

5-√3

• Hasil perasionalan

[tex]\frac{2\sqrt{5}}{5+\sqrt{3}}=\frac{2\sqrt{5}}{5+\sqrt{3}}\cdot\frac{5-\sqrt{3}}{5-\sqrt{3}}\\=\frac{2\sqrt{5}(5-\sqrt{3})}{5^2-(\sqrt{3})^2}\\=\frac{2\sqrt{5}(5-\sqrt{3})}{25-3}\\=\frac{2\sqrt{5}(5-\sqrt{3})}{22}\\=\frac{\sqrt{5}(5-\sqrt{3})}{11}\\=\frac{5\sqrt{5}-\sqrt{15}}{11}\\=\frac{5}{11}\sqrt{5}-\frac{1}{11}\sqrt{15}[/tex]

Untuk nomor 4:

• Bentuk sekawan penyebut

√3+√2

• Hasil perasionalan

[tex]\frac{4\sqrt{6}}{\sqrt{3}-\sqrt{2}}=\frac{4\sqrt{6}}{\sqrt{3}-\sqrt{2}}\cdot\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}\\=\frac{4\sqrt{6}(\sqrt{3}+\sqrt{2})}{(\sqrt{3})^2-(\sqrt{2})^2}\\=\frac{4\sqrt{18}+4\sqrt{12}}{3-2}\\=\frac{12\sqrt{2}+8\sqrt{3}}{1}\\=12\sqrt{2}+8\sqrt{3}[/tex]

Untuk nomor 5:

• Bentuk sederhana penyebut

2√2+3√3 = 5√3

• Hasil perasionalan

[tex]\frac{4+\sqrt{2}}{2\sqrt{3}+3\sqrt{3}}=\frac{4+\sqrt{2}}{5\sqrt{3}}\\=\frac{4+\sqrt{2}}{5\sqrt{3}}\cdot\frac{\sqrt{3}}{\sqrt{3}}\\=\frac{4\sqrt{3}+\sqrt{6}}{5\cdot3}\\=\frac{4\sqrt{3}+\sqrt{6}}{15}\\=\frac{4}{15}\sqrt{3}+\frac{1}{15}\sqrt{6}[/tex]

Materi tentang Merasionalkan Bentuk Akar pada https://brainly.co.id/tugas/42465739

#BelajarBersamaBrainly

#SPJ1

[tex]6 \times 5 \frac{6}{4} [/tex]

[tex]6 \times 5 \frac{3}{2} [/tex]

[tex]6 \times \frac{2 \times 5 + 3}{2} [/tex]

[tex]6 \times \frac{13}{2} [/tex]

[tex] \frac{6 \times 13}{2} [/tex]

[tex] \frac{78}{2} = \boxed{\bf\blue{39}}[/tex]