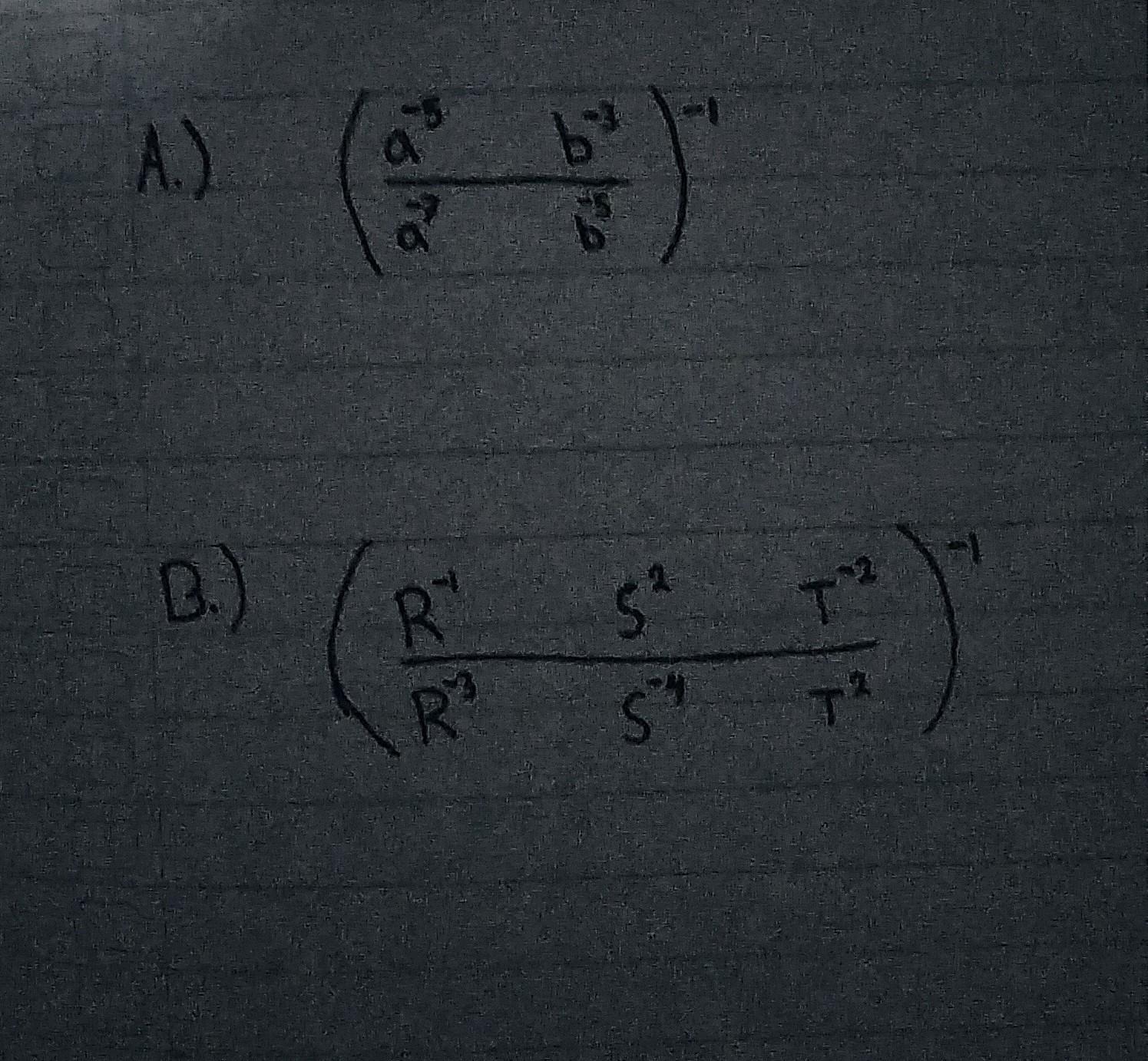soal limit tak hingga trigonometritolong penjelasannya lengkap yaa
-
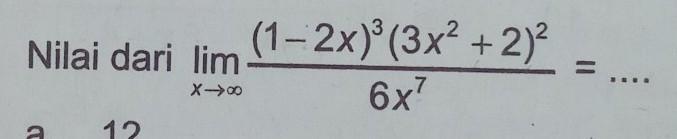
Bidang studi:
Matematika -
Penulis:
delilah43 -
Dibuat:
1 tahun lalu
Jawaban 1
Nilai limit tak hingga dari soal diatas adalah -12. Dimana dalam pengerjaannya pangkat tertingginya ada x⁷.
Penjelasan dengan langkah-langkah:
Untuk menyelesaikan soal limit tak hingga pada gambar diatas, maka terlebih dahulu diselesaikan persamaan pada pembilang
- (1 - 2x)³ = (1 - 2x) (1 - 2x) (1 - 2x) (1 - 2x)³ = -8x³ + 12x²- 6x +1
- (3x²+ 2)² = (3x²+ 2) (3x²+ 2)(3x²+ 2)² = 9x⁴+ 12x² + 4
- (-8x³ + 12x²- 6x +1) (9x⁴+ 12x² + 4) = -72x⁷ + 108x⁶ - 150x⁵+ 15x⁴ + 40x³ + 60x² - 24x + 4
Setelah didapatkan persamaan kuadrat pada pembilang sebagai berikut
[tex]\\ \lim_{x \to \infty} \frac{(1-2x)^{3} (3x^3+2)^2 }{6x^7}[/tex]
Untuk mendapatkan hasil dari limit tak hingga maka pembilang dan peneyebut dibagi dengan x dengan pangkat tertinggi, yaitu x⁷
[tex]=\lim_{x \to \infty} \frac{ -72x^{7} + 108x^{6} - 150x^{5} + 15x^{4} + 40x^{3} + 60x^{2} - 24x + 4}{6x^{7} }\\[/tex]×[tex]\frac{\frac{1}{x^{7} } }{\frac{1}{x^7} }[/tex][tex]=\lim_{x \to \infty} \frac{ \frac{-72x^{7}}{x^7} + \frac{ 108x^{6} }{x^7}- \frac{150x^{5}}{x^7} + \frac{15x^{4}}{x^7} + \frac{40x^{3}}{x^7} + \frac{60x^{2} }{x^7} - \frac{24x }{x^7} + \frac{4}{x^7} }{\frac{6x^{7}}{x^7} }\\[/tex][tex]=\frac{-72+0-0+0+0+0-0+0}{6} \\=\frac{-72}{6} \\=-12[/tex]
Pelajari lebih lanjut Pelajari lebih lanjut mengenai limit pada link berikut https://brainly.co.id/tugas/17317617
#BelajarBersamaBrainly#SPJ1
-
Penulis:
collin661
-
Nilai jawaban:
0
Apakah kamu tahu jawabannya? Tambahkan di sini!
Other related questions that may help you
-
Penulis:
wiggins
Penjelasan dengan langkah-langkah:
[tex]\mathbb{ \color{red}{ - \: R }}[/tex]
-
Penulis:
bluelavf
-
Nilai jawaban:
16
-
Penulis:
dahlia
-
Penulis:
milagrosblankenship
-
Nilai jawaban:
17
-
Penulis:
zippywkca
-
Nilai jawaban:
0
-
Penulis:
macintosh
-
Penulis:
kikiwhitaker
-
Nilai jawaban:
16
-
Penulis:
vaughnbean
-
Penulis:
yadielrvgm
-
Nilai jawaban:
5