Pada kubus ABCD.EFGH dengan rusuk 10 cm. Tentukan jarak bidang AFH ke bidang BDG.
-
Bidang studi:
Matematika -
Penulis:
lilianna -
Dibuat:
1 tahun lalu
Jawaban 1
AC = √AB²+BC²
= √10²+10²
= √100+100
= √200
= 10√2 cm
NC =½ AC
[tex] = \frac{1}{2} \times 10 \sqrt{2} [/tex]
[tex] = 5 \sqrt{2} [/tex]
GN=√GC²+NC²
=√10²+(5√2)²
=√100+50
=√150
= 5√6 cm
AN=NC=5√2 cm
NM=GC=AE=10 cm
[tex]pq = \frac{an.nm}{gn} \\ = \frac{5 \sqrt{2} .10 }{5 \sqrt{6} } \\ = \frac{10\sqrt{2} }{ \sqrt{6} } \\ = \frac{10 \sqrt{2} }{ \sqrt{6} } . \frac{ \sqrt{6} }{ \sqrt{6} } \\ = \frac{10 \sqrt{12} }{6} \\ = \frac{5}{3} \sqrt{12} [/tex]
[tex] = \frac{5}{3} \sqrt{12} [/tex]
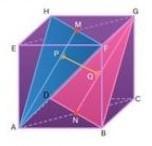
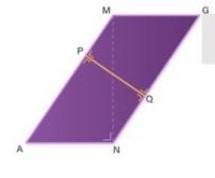
-
Penulis:
sanai0kbr
-
Nilai jawaban:
6
Apakah kamu tahu jawabannya? Tambahkan di sini!
Pilih bahasa dan wilayah
How much to ban the user?
1 hour
1 day
100 years


