Tujuan utama konsumen dalam mengonsumsi suatu produk atau barang dan jasa adalah untuk memaksimalkan kepuasan total (total utilyty) jelaskan apa yang dimaksud kepuasan total tersebut

Jawaban:

1.pengaturan proses-proses fisik, psikologis, dan perilaku seseorang, dengan kata lain serangkaian proses yang membentuk dirinya sendiri

2.Tidak mau menyalahkan orang lain maupun keadaan,Berjiwa optimis tidak mudah putus asa,Suka belajar dan mau melihat kekurangan dirinya

3.kemampuan seseorang mengendalikan dirinya sendiri dimana kontrol perilakunya dipegang oleh dirinya sendiri / menahan diri dari segala perilaku yg dapat merugikaan diri sendiri dan juga orang lain

4.minat,cita cita,Motivasi ekstrinsik: kepemimpinan, upah, lingkungan (sarana dan prasarana, penasehat akademik, iklim kerja)

5.Hal ini karena siswa sendirilah yang akhirnya mengambil keputusan tentang apa yang hendak dilakukan dan bertanggung jawab atas hasil belajarnya

6.Cari Suasana yang Tepat,Belajar Bersama Teman,dengarkan dan lakukan motivasi yang disampaikan dengan orang lain selagi itu benar

Penjelasan:

semoga membantu && maaf kalau ada yang salah ^^

Koordinat untuk tabel fungsi [tex]y = x^2 \:+\: 2x[/tex] adalah

• (- 3 , 3)
• (- 2 , 0)
• (- 1 , - 1)
• (0 , 0)
• (1 , 3)
• (2 , 8)
• (3 , 15)

Koordinat untuk tabel fungsi [tex]y = - x^2 \:-\: 2x[/tex] adalah

• (- 3 , - 3)
• (- 2 , 0)
• (- 1 , 1)
• (0 , 0)
• (1 , - 3)
• (2 , - 8)
• (3 , - 15)

Grafik persamaan kuadrat pertama dan kedua ada di lampiran pertama. Grafik persamaan kuadrat ketiga dan keempat ada di lampiran kedua.

GRAFIK FUNGSI KUADRAT

Cara pertama untuk membuat grafik persamaan kuadrat adalah:

• Dengan mensubtitusi beberapa nilai x ke dalam persamaan untuk mendapatkan nilai y.
• Setelah mendapatkan beberapa pasangan koordinat, lalu hubungkan semua titik koordinat yang diperoleh.

Cara kedua untuk membuat grafik persamaan kuadrat adalah:

• Menentukan koordinat titik potong dengan sumbu x dimana y = 0.
• Menentukan koordinat titik potong dengan sumbu y dimana x = 0.
• Menentukan koordinat titik puncak grafik dimana y = f(x) = ax² + bx + c berlakuKoordinat titik puncak = [tex](\frac{- b}{2a} \:,\: \frac{b^2 \:-\: 4ac}{- 4a})[/tex]
• Hubungkan titik-titik koordinat yang diperoleh.

Penjelasan dengan langkah-langkah:

Diketahui:

• 1.A. [tex]y = x^2 \:+\: 2x[/tex]
• 1.B. [tex]y = - x^2 \:-\: 2x[/tex]
• 2.A. f(x) = [tex]x^2 \:-\: 6x \:+\: 5[/tex]
• 2.B. f(x) = [tex]- x^2 \:+\: 5x \:-\: 4[/tex]

Ditanyakan:

1. Isilah tabel dan gambar grafiknya!
2. Sketsa grafik?

Jawaban:

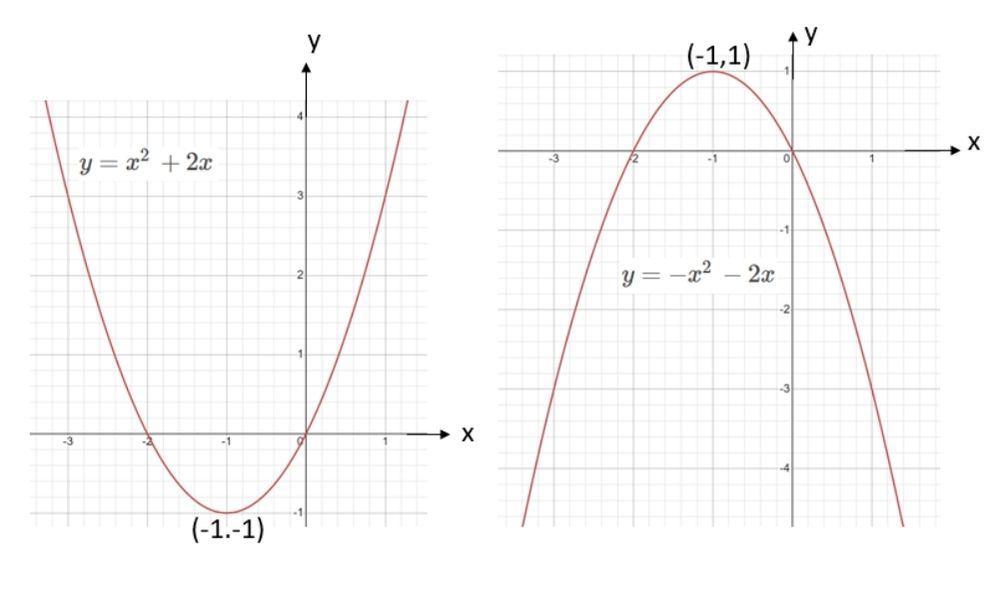
Menentukan tabel untuk [tex]y = x^2 \:+\: 2x[/tex].

• x = - 3[tex]y = (- 3)^2 \:+\: 2 (- 3) \:=\: 9 \:-\: 6 \:=\: 3[/tex](- 3 , 3)
• x = - 2[tex]y = (- 2)^2 \:+\: 2 (- 2) \:=\: 4 \:-\: 4 \:=\: 0[/tex](- 2 , 0)
• x = - 1[tex]y = (- 1)^2 \:+\: 2 (- 1) \:=\: 1 \:-\: 2 \:=\: - 1[/tex](- 1 , - 1)
• x = 0[tex]y = (0)^2 \:+\: 2 (0) \:=\: 0 \:+\: 0 \:=\: 0[/tex](0 , 0)
• x = 1[tex]y = (1)^2 \:+\: 2 (1) \:=\: 1 \:+\: 2 \:=\: 3[/tex](1 , 3)
• x = 2[tex]y = (2)^2 \:+\: 2 (2) \:=\: 4 \:+\: 4 \:=\: 8[/tex](2 , 8)
• x = 3[tex]y = (3)^2 \:+\: 2 (3) \:=\: 9 \:+\: 6 \:=\: 15[/tex](3 , 15)

Gambar grafik ada di lampiran pertama sebelah kiri.

Menentukan tabel untuk [tex]y = - x^2 \:-\: 2x[/tex].

• x = - 3[tex]y = - (- 3)^2 \:-\: 2 (- 3) \:=\: - 9 \:+\: 6 \:=\: - 3[/tex](- 3 , - 3)
• x = - 2[tex]y = - (- 2)^2 \:-\: 2 (- 2) \:=\: - 4 \:+\: 4 \:=\: 0[/tex](- 2 , 0)
• x = - 1[tex]y = - (- 1)^2 \:-\: 2 (- 1) \:=\: - 1 \:+\: 2 \:=\: 1[/tex](- 1 , 1)
• x = 0[tex]y = - (0)^2 \:-\: 2 (0) \:=\: - 0 \:-\: 0 \:=\: 0[/tex](0 , 0)
• x = 1[tex]y = - (1)^2 \:-\: 2 (1) \:=\: - 1 \:-\: 2 \:=\: - 3[/tex](1 , - 3)
• x = 2[tex]y = - (2)^2 \:-\: 2 (2) \:=\: - 4 \:-\: 4 \:=\: - 8[/tex](2 , - 8)
• x = 3[tex]y = - (3)^2 \:-\: 2 (3) \:=\: - 9 \:-\: 6 \:=\: - 15[/tex](3 , - 15)

Gambar grafik ada di lampiran pertama sebelah kanan.

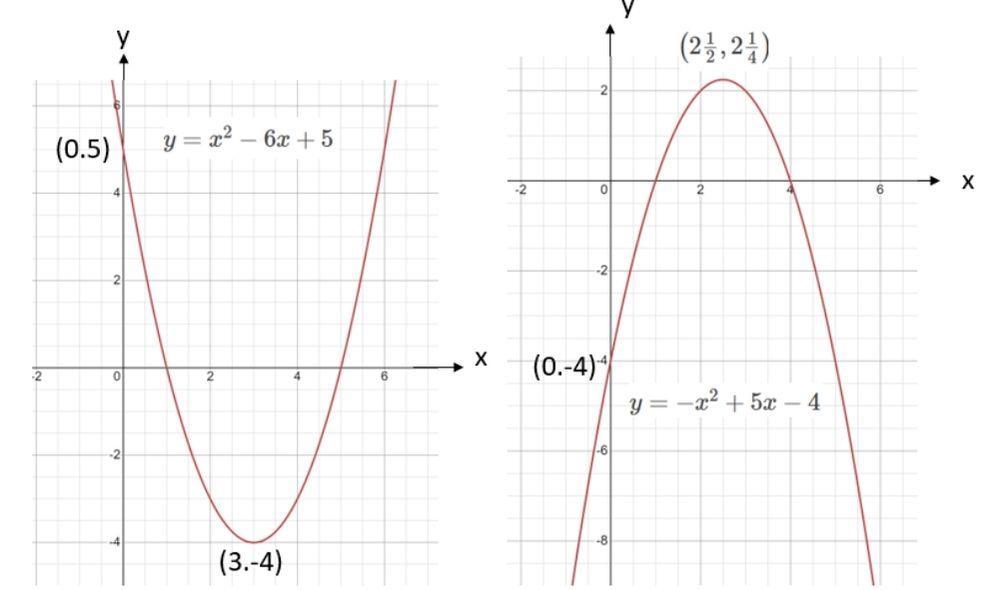
Membuat sketsa grafik f(x) = [tex]x^2 \:-\: 6x \:+\: 5[/tex].

• Titik potong dengan sumbu x.y = [tex]x^2 \:-\: 6x \:+\: 5[/tex]0 = [tex]x^2 \:-\: 6x \:+\: 5[/tex]0 = [tex]x^2 \:-\: 5x \:-\: x \:+\: 5[/tex]0 = tex]x \: (x \:-\: 5) \:-\: 1 \: (x \:-\: 5)[/tex]0 = (x - 5) (x - 1)x - 5 = 0  atau x - 1 = 0x = 5        atau x = 1(5 , 0) dan (1 , 0)
• Titik potong dengan sumbu y.y = [tex]x^2 \:-\: 6x \:+\: 5[/tex]y = [tex]0^2 \:-\: 6 \: (0) \:+\: 5[/tex]y = 0 - 0 + 5y = 5(0 , 5)
• Koordinat titik puncak.a = 1b = - 6c = 5[tex](\frac{- b}{2a} \:,\: \frac{b^2 \:-\: 4ac}{- 4a})[/tex]= [tex](\frac{6}{2 \times 1} \:,\: \frac{(- 6)^2 \:-\: (4 \times 1 \times 5)}{- 4 \times 1)})[/tex]= [tex](\frac{6}{2} \:,\: \frac{36 \:-\: 20}{- 4})[/tex]= (3 , [tex]\frac{16}{- 4}[/tex])= (3 , - 4)

Sketsa grafik ada pada lampiran kedua sebelah kiri.

Membuat sketsa grafik f(x) = [tex]- x^2 \:+\: 5x \:-\: 4[/tex]

• Titik potong dengan sumbu x.y = [tex]- x^2 \:+\: 5x \:-\: 4[/tex]0 = [tex]- x^2 \:+\: 5x \:-\: 4[/tex]0 = (- x + 4) (x - 1)- x + 4 = 0  atau  x - 1 = 0x = 4          atau  x = 1(4 , 0) dan (1, 0)
• Titik potong dengan sumbu y.y = [tex]- x^2 \:+\: 5x \:-\: 4[/tex]y = [tex]- 0^2 \:+\: 5 \: 0 \:-\: 4[/tex]y = 0 + 0 - 4y = - 4(0 , - 4)
• Koordinat titik puncak.a = - 1b = 5c = - 4[tex](\frac{- b}{2a} \:,\: \frac{b^2 \:-\: 4ac}{- 4a})[/tex]= [tex](\frac{- 5}{2 \times - 1} \:,\: \frac{5^2 \:-\: (4 \times - 1 \times - 4)}{- 4 \times - 1})[/tex]= [tex](\frac{- 5}{- 2} \:,\: \frac{25 \:-\: 16}{4})[/tex]= [tex](- 2\frac{1}{2} \:,\: \frac{9}{4})[/tex]= [tex](- 2\frac{1}{2} \:,\: 2 \frac{1}{4})[/tex]

Sketsa grafik ada pada lampiran kedua sebelah kanan.

Pelajari lebih lanjut

• Materi tentang Persamaan Kuadrat https://brainly.co.id/tugas/26029986
• Materi tentang Koordinat Titik Puncak https://brainly.co.id/tugas/36151468
• Materi tentang Grafik Persamaan Kuadrat https://brainly.co.id/tugas/33816341

Detail Jawaban

Kelas : VIII

Mapel : Matematika

Bab : Fungsi

Kode : 8.2.2.

#TingkatkanPrestasimu

#SPJ6

Jawaban:

B.sedikit condong ke belakang

Penjelasan:

maaf kalau bener/salah

semoga terserahmu

8/1, 16/2, 24/3, 40/5

Jawab:

A. 56/7 = 56÷7/7÷7 = 8/1 = 8 (Senilai dengan 8)

B. 48/6 = 48÷6/6÷6 = 8/1 = 8 (Senilai dengan 8)

C. 24/3 = 24÷3/3÷3 = 8/1 = 8 (Senilai dengan 8)

FOLLOW dn TERIMAKASIH jika benar