TOLONG DI JAWAB YA KAK TOLONG SECEPATNYAJAWAB YANG BENER√​

Jawaban:

teman teman

manis

baru datang

Pendapat mengenai hal tersebut adalah ciri yang tersebut pada soal sudah sesuai dengan ciri orang yang bekerja keras. Di mana orang yang bekerja kerja selalu berusaha sesegera mungkin untuk melakukan sesuatu.

Berkerja atau berusaha terhadap sesuatu dalam islam dikenal dengan istilah ikhtiar. Ikhtiar harus dilakukan oleh setiap umat manusia dalam kehidupan sehari-hari agar dapat merubah kehidupannya. Hal ini karena dalam salah satu ayat menyebutkan bahwa Allah tidak merubah nasib satu kaum jika kaum tersebut tidak berusaha atau tidak berikhtiar untuk mengubah nasib yang dimilikinya.

Pelajari lebih lanjut materi tentang ikhtiar https://brainly.co.id/tugas/2094146

#BelajarBersamaBrainly #SPJ1

Jawaban:

7 2/4

Penjelasan dengan langkah-langkah:

maaf klo salah q(❂‿❂)p

Jawaban:

[tex]7 \frac{2}{4} \div \frac{2}{2} = 7 \frac{1}{2} [/tex]

Penjelasan dengan langkah-langkah:

Jawabannya A

makasii

#terimakasihatasperhatiannya

Hasil dari perpangkatan berikut adalah:

• a. (x⁴/x³)² = x²
• b. (6x⁸y¹¹)/(2x²y)³ = ¾ x²y⁸
• c. 2⁸/2⁵ = 8
• d. 3⁴ × 3² = 729
• e. (–h³)² = h⁶

1. Diketahui

[tex]a. \: \left(\frac{x^{4}}{x^{3}}\right)^{2}[/tex]

[tex]b. \: \frac{6x^{8}y^{11}}{(2x^{2}y)^{3}}[/tex]

[tex]c.\: \frac{2^{8}}{2^{5}}[/tex]

[tex]d.\: 3^{4} \times 3^{2}[/tex]

[tex]e. \: (-h^{3})^{2}[/tex]

Ditanyakan

Selesaikan bentuk pangkat tersebut!

Jawab

[tex]a. \: \left(\frac{x^{4}}{x^{3}}\right)^{2}[/tex]

   [tex]= (x^{4 - 3})^{2}[/tex]

   [tex]= (x^{1})^{2}[/tex]

   [tex]= x^{2}[/tex]

[tex]b. \: \frac{6x^{8}y^{11}}{(2x^{2}y)^{3}}[/tex]

   [tex]= \frac{6x^{8}y^{11}}{2^{3}x^{6}y^{3}} [/tex]

   [tex]= \frac{6}{8} \: x^{8-6} \: y^{11-3}[/tex]

   [tex]= \frac{3}{4} \: x^{2} \: y^{5}[/tex]

[tex]c.\: \frac{2^{8}}{2^{5}}[/tex]

   [tex]= 2^{8 - 5}[/tex]

   [tex]= 2^{3}[/tex]

   [tex]= 8[/tex]

[tex]d.\: 3^{4} \times 3^{2}[/tex]

   [tex]= 3^{4+2}[/tex]

   [tex]= 3^{6}[/tex]

   [tex]= 729[/tex]

[tex]e. \: (-h^{3})^{2}[/tex]

   [tex]= h^{6}[/tex]

2. Diketahui

• a. x⁻⁵
• b. 3x⁻⁷
• c. (4² + 3²)⁻¹

Ditanyakan

Ubah dalam pangkat positif!

Jawab

• [tex]a. \: x^{-5} = \frac{1}{x^{5}}[/tex]
• [tex]b. \: 3x^{-7} = \frac{3}{x^{7}}[/tex]
• [tex]c. \: (4^{2} + 3^{2})^{-1} = \frac{1}{4^{2} + 3^{2}}[/tex]

3. Diketahui

• a. 2x⁰ + 3y⁰
• b. 9x⁰
• c. a⁰ + b⁰ + c⁰

Ditanyakan

Sederhanakan bentuk pangkat tersebut!

Jawab

a. 2x⁰ + 3y⁰ = 2(1) + 3(1)

                     = 2 + 3

                     = 5

b. 9x⁰ = 9(1)

          = 9

c. a⁰ + b⁰ + c⁰ = 1 + 1 + 1

                      = 3

4. Diketahui

• [tex]a. \: \frac{1}{a^{2}}[/tex]
• [tex]b. \: \frac{1}{4y^{6}}[/tex]
• [tex]c. \: \frac{5}{(a \:+\: b)^{3}}[/tex]

Ditanyakan

Ubah dalam bentuk pangkat negatif!

Jawab

• [tex]a. \: \frac{1}{a^{2}} = a^{-2}[/tex]
• [tex]b. \: \frac{1}{4y^{6}} = \frac{y^{-6}}{4}[/tex]
• [tex]c. \: \frac{5}{(a \:+\: b)^{3}} = 5(a \:+\: b)^{-3}[/tex]

5. Diketahui

f(x) = 3x

Ditanyakan

Gambarlah grafik dari fungsi tersebut!

Jawab

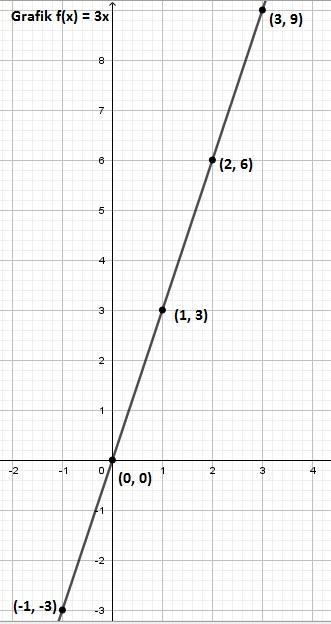
Kita ambil daerah asal dari f(x) adalah x = {–1, 0, 1, 2, 3}. Substitusi daerah asal tersebut ke f(x) untuk mencari titik-titik yang dilalui grafik tersebut.

• f(–1) = 3(–1) = –3 ⇒ (–1, –3)
• f(0) = 3(0) = 0 ⇒ (0, 0)
• f(1) = 3(1) = 3 ⇒ (1, 3)
• f(2) = 3(2) = 6 ⇒ (2, 6)
• f(3) = 3(3) = 9 ⇒ (3, 9)

Hubungkan titik-titik yang diperoleh sehingga membentuk garis lurus kemudian perpanjang. Garis itulah yang merupakan grafik dari f(x) = 3x. Gambar dapat dilihat di lampiran.

Materi tentang pangkat pecahan https://brainly.co.id/tugas/7415917

#BelajarBersamaBrainly #SPJ1